Il Tapa (Turkish Art Paint) è un puzzle che rivela una lontana somiglianza con il Sudoku, anche se non proviene dalla creatività giapponese. A idearlo è stato infatti nel 2007 il geniale turco Serkan Yürekli. Nel blog The art of puzzles una sezione è dedicata proprio a questo gioco.
Ho scoperto il Tapa grazie alla rubrica Can you solve it del Guardian. In Italia non mi risulta sia ancora arrivato.
Quali sono le regole del Tapa? Vediamole, insieme alle principali strategie di risoluzione.
La disposizione iniziale
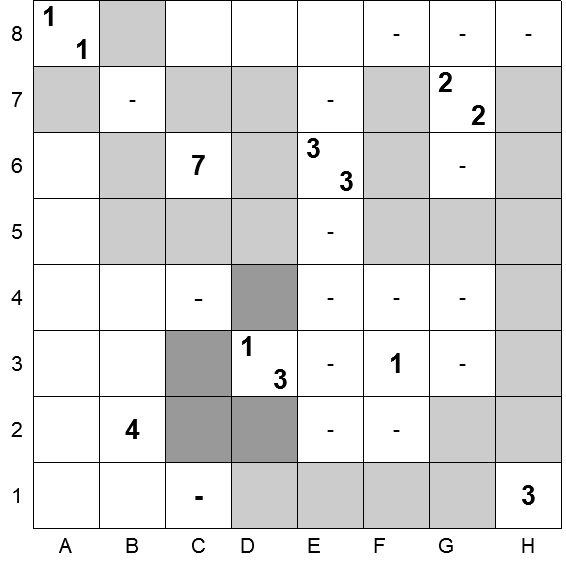
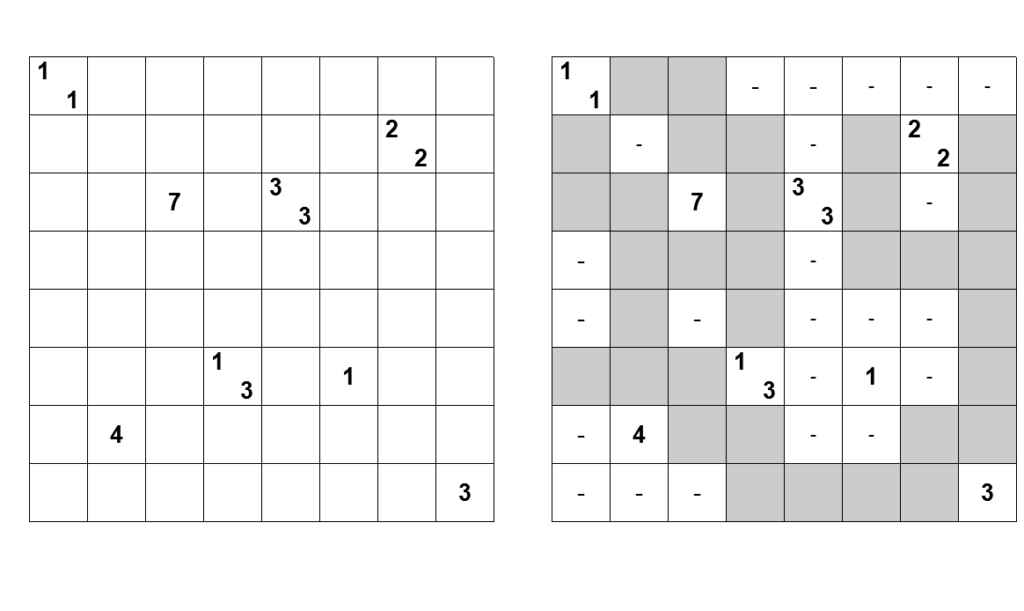
L’immagine a lato riporta un esempio di Tapa da risolvere (tratto dalla rubrica del Guardian).
La griglia è generalmente quadrata, ma può essere anche rettangolare ed esistono inoltre variazioni con forme poligonali.
Anche le dimensioni della griglia possono variare con libertà. Perché una griglia quadrata assicuri un divertimento adeguato, le dimensioni saranno almeno di 8 × 8 celle, come nell’esempio a lato.
Nota: le coordinate 1-8 e A-H sono state inserite solo come guida per questo post.
Lo scopo del gioco è quello di annerire una parte delle celle della griglia, in base alle indicazioni contenute in alcune celle, e, ovviamente, alle regole del Tapa.
Vediamo come leggere le indicazioni.
Una cella lontana dai bordi è circondata da 8 celle (due in verticale, due in orizzontale e quattro in diagonale). I numeri eventualmente contenuti in una cella indicano quante celle vicine vanno annerite, e forniscono indicazioni su come sono disposte queste celle.
Nella cella 2B, ad esempio, il “4” indica che, delle 8 celle vicine, ne sono annerite 4 contigue, in un’unica sequenza.
Le celle vicine ai bordi hanno meno vicini. Quella in alto a sinistra, ad esempio, che contiene “1 1“, ha solo tre celle vicine. Bene, “1 1” indica che le tre celle saranno occupate da due sequenze di neri, ciascuna di una cella sola. C’è sempre almeno una cella vuota a separare due sequenze.
Allo stesso modo un’indicazione “1 1 2” avrebbe indicato tre sequenze di celle annerite, rispettivamente di 1, 1 e 2 celle.
Variazioni del Tapa
Ci sono almeno un paio di variazioni del gioco che vale la pena di segnalare.
La prima: l’indicazione può contenere dei “?”, come ad esempio: “1 ? 1“, che indica tre sequenze di celle annerite, di cui una è di lunghezza non nota.
Oppure le indicazioni contenute nelle colonne e nelle righe sono riportate tutte insieme fuori griglia, all’inizio rispettivamente della colonna o della riga. In questo caso occorre quindi anche capire a quale cella si riferisca ciascuna indicazione.
Le regole del Tapa
Le regole da seguire sono abbastanza semplici:
- annerire le celle, secondo le indicazioni contenute nella griglia; le celle recanti indicazioni non vanno annerite;
- tutte le celle annerite devono essere connesse tra loro lungo uno o più lati, in un unico corpo nero; condividere un vertice non costituisce connessione;
- non possono esserci 4 celle annerite a formare un quadrato.
Le prime mosse
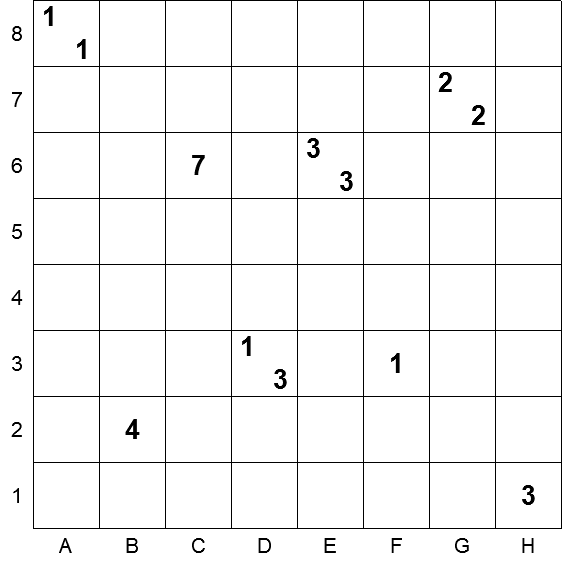
Una regola di base nei giochi di questo tipo è quella di effettuare per prime le mosse più ovvie. Saranno queste mosse a semplificare il lavoro successivo.
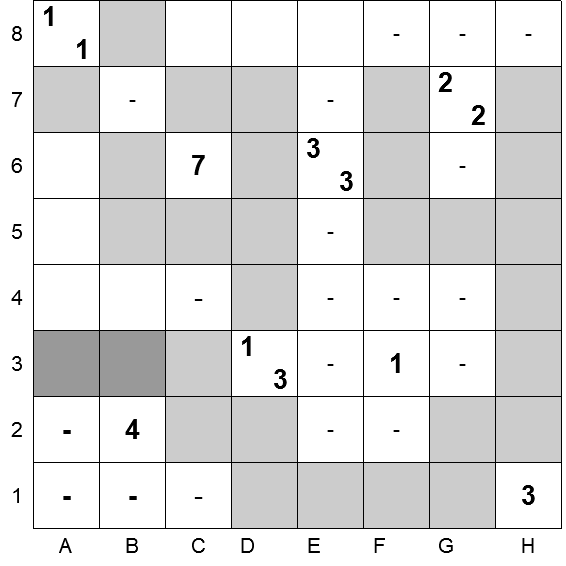
Nel nostro esempio, è bene partire dalle celle A8 e 1H.
Per la prima, la sola combinazione possibile per le tre celle vicine è, partendo da quella in alto a destra e procedendo in senso orario: “N – N“, vale a dire: una cella nera, una vuota, una nera.
Per la cella 1H la sola sequenza possibile è ancora più semplice: “N N N“.
In questa immagine e in quelle successive, si marcheranno con un grigio più scuro e con un simbolo “–” in grassetto le celle la cui colorazione viene determinata in quel momento.
Altre due celle facili
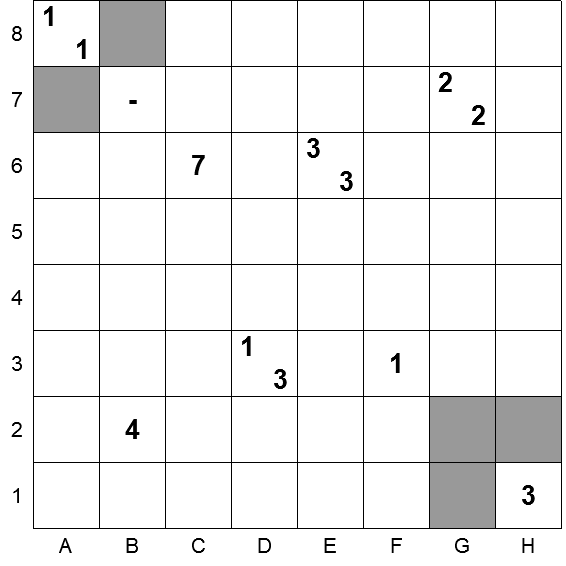
Aver risolto le celle A8 e 1H aiuta a risolvere le celle 6C e 3F.
Infatti:
- la cella 3F ha un solo vicino annerito, che è stato già determinato; quindi gli altri 7 vicini sono vuoti;
- simmetricamente, la cella 6C ha 7 celle vicine annerite e solo una vuota, già determinata.
La griglia comincia a popolarsi!
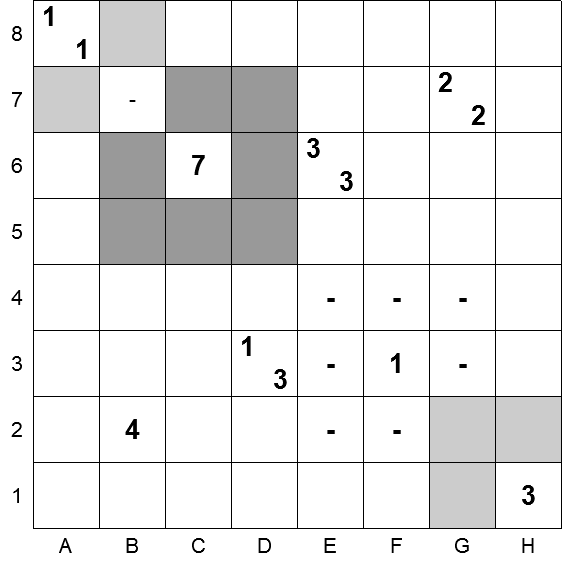
Inoltre abbiamo adesso elementi per affrontare la cella 6E, che a sua volta ci aprirà la strada per la cella 7G.
Per la prima il ragionamento è ancora semplice: delle due sequenze da 3, una è già tracciata. L’altra (vedi figura successiva) è determinata dopo aver marcato le due celle vuote che separano le due sequenze da 3.
Ora serve qualche ragionamento più sottile
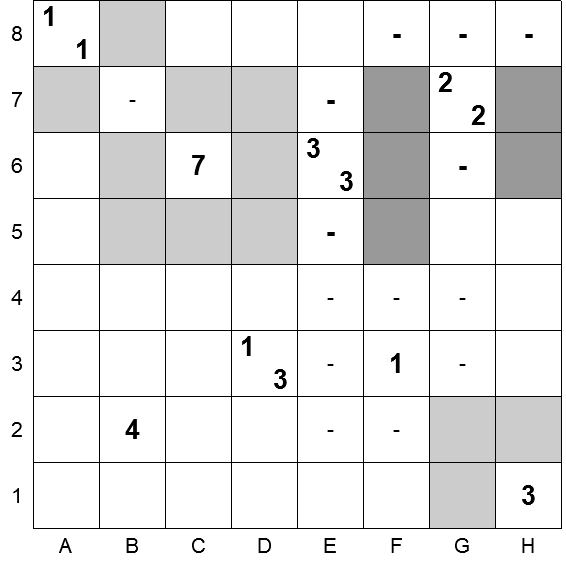La faccenda si fa più complicata per la cella 7G.
Delle due sequenze da 2 che circondano la cella 7G, una è già tracciata (6F-7F). Di conseguenza le celle 6G e 8F sono vuote.
Occorre quindi, nelle 4 celle rimanenti, piazzare una sequenza da 2 e 2 celle vuote.
Un’osservazione utile è che, a questo punto, la possibilità di connettere le celle annerite a sinistra della colonna E con quelle a destra della stessa colonna passa per un’unica cella, la 1E.
Si proceda per esclusione.
Una sequenza piazzata in 8G – 8H rimarrebbe isolata, violando la regola n.ro 2 (le celle devono essere connesse).
Lo stesso avverrebbe se la sequenza fosse posizionata in 8H – 7H. Quindi la posizione corretta è 7H – 6H.
Cominciamo a unire le celle
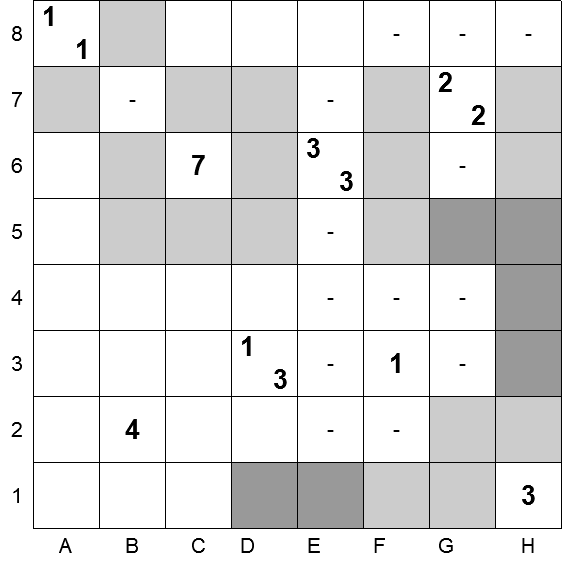È arrivato il momento di connettere le celle annerite poste a destra della colonna E; prima tra loro e, poi, verso il lato a sinistra della colonna stessa.
Anneriamo quindi in sequenza:
- 5G e 5H, per unire le due isole nere in alto;
- 4H e 3H, per unire l’isola superiore con quella inferiore;
Infine anneriamo le celle 1D e 1E, per portarci a sinistra della colonna E.
Per nessuna di queste celle c’erano indicazioni di riempimento.
Siamo quasi in dirittura d’arrivo
Manca ormai da seguire solo le indicazioni delle celle 3D e 4B.
Intorno alla cella 3D sono rimaste 5 celle utili, in cui va sistemata una sequenza da 3, una da 1 e una cella vuota.
Ora, almeno una tra le celle 4C e 4D deve essere annerita, ma non tutte e due, altrimenti si formerebbe un quadrato annerito con le due celle sovrastanti (regola n.ro 3, del quadrato).
Quindi va annerita 4D, in modo da lasciare vuota la 4C, e consentire la sequenza da 3 nelle celle 3C – 2C – 2D.
Infine completare i vicini della cella 2B è immediato. La cella 1C introduce la sequenza da 4 celle annerite, di cui 2 sono già tracciate. Non resta che annerire 2C e 2D, e marcare come vuote le altre.
Ultime celle!
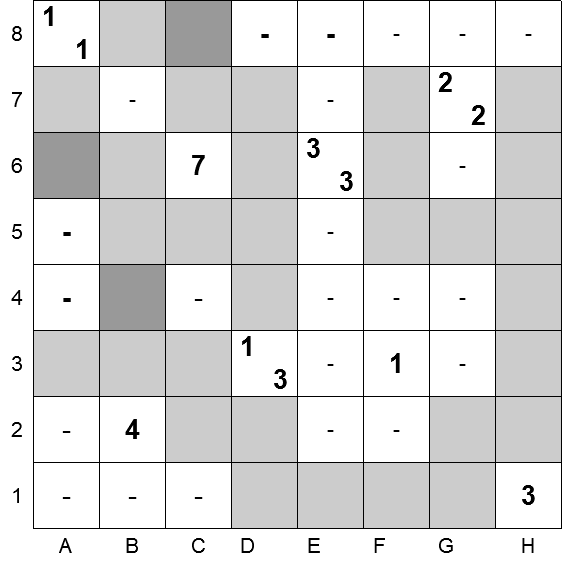Rimane da determinare lo stato delle celle 8C – 8D – 8E, e delle celle 6A – 5A – 4A – 4B.
La cella 8C va annerita, per connettere la cella 8B che al momento è isolata. Le celle 8D – 8E, invece, devono restare vuote, la prima per la regola del quadrato, la seconda per non rimanere isolata.
Stesso tipo di ragionamento per le restanti celle:
- 6A va annerita, per connettere la cella 7A;
- 4B va annerita, per connettere la cella 5B (e le celle collegate direttamente o indirettamente) con la cella 3B e quindi il resto del corpo nero;
- le celle 5A – 4A devono rimanere vuote (regola del quadrato).
Il quadro è completato!
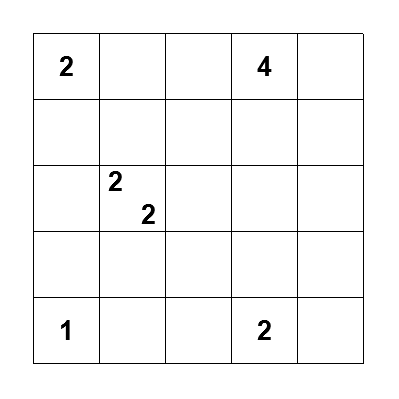Non si trovano molti esempi in rete di Tapa. Qualcosa c’è su janko.at, sito in tedesco e quindi per me incomprensibile.
Proprio da janko.at si può cominciare, iniziando con i Tapa più semplici, come quello riportato nella figura a lato. Non c’è bisogno di trascriverlo, si può giocare direttamente via web: click ripetuti su una cella la marcano come annerita, vuota, ancora da determinare.
Se avete notizia di altro materiale, segnalatemelo nei commenti! Io farò lo stesso.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
