Tra il 1200 e il 1600, un’autentica rivoluzione trasforma il modo con cui, in Occidente, si rappresentano e si manipolano i numeri.
Nella rivoluzione dello zero, prima compaiono le cifre e lo zero, nate in India e diffuse in Occidente dagli Arabi. Poi è il turno dei simboli delle operazioni: le quattro fondamentali, la radice quadrata, gli esponenti. Il tutto velocizza il calcolo e supporta lo sviluppo dei commerci in un mondo che comincia a diventare, se non globale, almeno molto più aperto. E, inoltre, pone le basi per lo sviluppo della matematica negli anni a venire.
L’esigenza di contare
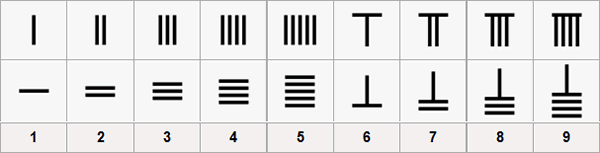
La rappresentazione dei numeri nasce con la necessità di inventariare animali, soldati, grano. In questa prima fase basta contare, e il modo più semplice per farlo è quello di associare una tacca a un elemento da contare.
La prima esigenza che nasce è quella di mantanere compatta la rappresentazione. Nascono così simboli per raggruppare un determinato numero di tacche. Essendo le nostre mani dotate di dieci dita, i raggruppamenti più intuitivi sono quelli per 10 e multipli e divisori di 10.
L’esempio più evidente di questo semplice modo di contare è il sistema romano: l’unità (I), la cinquina (V), la decina (X), 50 (L), 100 (C), 500 (D), 1.000 (M). Numeri come 3.500 (MMMD) o 1.756 (MDCCLVI) erano già grandi per le esigenze degli antichi romani. Nel caso fosse stato necessario andare oltre, comunque, gli antichi romani utilizzavano un simbolo di moltiplicazione per 1.000, consistente nell’aggiunta di una lineetta sul simbolo numerico.
Per farsi un’idea di cosa volesse dire grande numerosità duemila anni fa, basta ricordare che una miriade indicava appena 10.000 unità. Uno stadio calcistico con una miriade di spettatori, oggi, è cosa appena normale!
Un sistema di numerazione come quello romano non è compatto, nonostante il trucco di rendere negativo il valore di un simbolo anteposto a uno di valore maggiore. Esempio, 4 si rappresenta con IV e non con IIII.
Ma soprattutto il sistema si presta male all’esecuzione di calcoli. Quanto fa MDCCLVI sommato a CCXLIV? Fa MM, ma arrivarci non è semplice.
I sistemi posizionali
Un modo per superare i difetti del sistema utilizzato dagli antichi romani è quello di utilizzarne uno posizionale, necessaria premessa perché possa avvenire poi la rivoluzione dello zero.
Un esempio di tale numerazione è quello utilizzato dai Babilonesi, antecedenti dei Romani (siamo nel 1700 a.C. circa).
I simboli elementari utilizzati sono solo due (vedere la rappresentazione di 1 e di 10).
Il sistema appare molto compatto e, se si aggiunge che i due simboli vengono lasciati in modo molto semplice da uno stilo su una tavoletta di argilla, non si può non ammirare l’ingegnosità dei Babilonesi.
Una delle migliaia di frammenti di tavoletta trovati presso la città babilonese di Nippur ci mostra come funzionava il sistema posizionale.
La tavoletta riporta la tabellina del 9, di scolastica memoria. Nella prima colonna sono riportati in progressione i numeri da 1 in avanti, nella seconda i relativi multipli di 9. Nella 7a riga si trova il multiplo di 7, che è 63. Se si osserva come è rappresentato 63, si vede che è la giustapposizione del simbolo dell’unità, uno spazio, il simbolo di 3 unità. Si intuisce che le tacche riportano 60 + 3.
Il sistema babilonese era infatti basato sul valore posizionale delle cifre e su una base di numerazione di 60. Una tacca quindi può rappresentare 1, 60, 602, e così via.
Un sistema posizionale rende ragionevolmente agili le quattro operazioni, magari con il supporto di tabelline. Aver scelto come base di numerazione 60, che ha un gran numero di sottomultipli, poi, semplifica la manipolazione di frazioni. Il tutto molto efficace per i Babilonesi, che con questo sistema progredirono notevolmente nell’astronomia. Da lì proviene il nostro conteggio dell’ora divisa in 60 minuti, ciascuno di 60 secondi.
Ma manca ancora qualcosa
In un sistema posizionale occorre rappresentare anche l’assenza di una potenza della base. Ad esempio, 60 + 1 e 602 + 1 differiscono solo per un buco da lasciare nel rappresentare il secondo numero.
I Babilonesi risolsero lasciando uno spazio, addizionale rispetto a quello che separa le potenze della base. Funziona con una calligrafia regolare, ma può rendere ambigua la lettura di un numero come 603 + 1, in cui devo lasciare un buco per la separazione delle basi e due per l’assenza della potenza 60 e 602.
Una possibile soluzione fu escogitata in Cina, all’epoca della Prima Dinastia Han (siamo intorno al 100 a.C.).
Sistema posizionale in base 10, con simboli che utilizzavano dei bastoncini, verticale per l’unità, orizzontale per la cinquina. Per rappresentare 7, ad esempio, venivano utilizzati due bastoncini verticali affiancati, posti sotto un bastoncino orizzontale.
L’assenza di una potenza era rappresentata ancora da un buco, ma, e qui sta la genialità del sistema, l’orientamento dei simboli era alternato da una cifra a quella contigua. Quindi per rappresentare 70, ad esempio, sarebbero stati utilizzati due bastoncini orizzontali sovrapposti, sotto un bastoncino verticale. In questo modo era consentita una maggiore elasticità nella scrittura del buco, perché l’errore di lettura era possibile solo confondendo un buco con tre.
Un bel passo in avanti, anche se non era ancora la soluzione. Rimaneva, ad esempio, il problema di indicare senza ambiguità il numero di posizioni vuote alla fine del numero.
(Qui la descrizione del sistema di numerazione attuale cinese.)
La rivoluzione dello zero, dall’India arriva la soluzione perfetta
Si deve all’ingegnosità degli Indiani l’aver superato i due problemi dei sistemi posizionali visti finora.
Il primo: come marcare l’assenza di una potenza?
Oggi è intuitivo dire che nessun oggetto vuol dire zero oggetti, ma l’umanità ha impiegato un po’ a creare questa associazione, creando un valore di conteggio anche in assenza di oggetti.
Scritto in numerazione corrente, 304 vuol dire tre centinaia, zero decine, quattro unità. Semplice, chiaro, senza possibili ambiguità.
Una volta inventato, però, lo zero si impone come concetto chiarissimo e risolutivo. Talmente importante da dare il suo nome (sefr) all’intero sistema delle cifre.
Il secondo problema: semplificazione dei simboli
Sia con il sistema babilonese che con quello cinese, la lettura di un numero comporta l’identificazione dei simboli mediante il conteggio di cunei impressi dallo stilo o bastoncini tracciati sul foglio.
Nel sistema indiano, una volta ridotti i simboli necessari a 9 (per identificare le cifre da 1 a 9), più lo zero, ogni cifra ha il suo semplice simbolo.
Messe tutte insieme, sistema posizionale, semplificazione dei simboli e zero, rendono finalmente semplice rappresentare e manipolare un numero di qualsivoglia grandezza. Fino alle miriadi, di miriadi, di miriadi e oltre.
Dall’India agli Arabi
Intorno all’800 l’impero islamico si espande fino a comprendere parte dell’India. È l’occasione per le conoscenze matematiche indiane di contaminare le menti arabe ed espandersi.
Muhammad ibn Musa al-Khwarizmi, matematico arabo dal cui nome deriva la parola algoritmo, tratta nei suoi libri sia del sistema di numerazione indiano, che del metodo, sempre ideato in India, della risoluzione di equazioni, mediante la manipolazione dei sue membri. La parola araba per descriverla è al-jabr, da cui deriva il nostro termine algebra.
La contaminazione risale la Spagna, e si diffonde nel resto dell’Europa.
In Italia, a contribuire in modo determinante all’introduzione della nuova numerazione è Leonardo Pisano detto il Fibonacci.
Non c’è storia, il farraginoso sistema di numerazione romano lascia il campo ai numeri arabi (o indiani). Rimarrà solo per rappresentare gli ordinali (ricordate di quando avete frequentato la V elementare?), i paragrafi dei testi avvocatizi e come opzione negli elenchi puntati di Word e Power Point.
Dopo la rivoluzione dello zero, è il turno dei simboli delle operazioni
Una volta in campo un sistema di numerazione finalmente semplice ed efficace, l’attenzione si spostò sul semplificare e razionalizzare il modo per rappresentare le operazioni.
In un’equazione, infatti, vanno rappresentati dei numeri, una o più incognite, ma anche delle operazioni di somma, sottrazione, moltiplicazione o divisione, e capita anche di dover indicare l’estrazione di radici. Ognuna di queste operazioni può essere descritta in modo verbale o, più concisamente, da un simbolo.
L’invenzione della stampa (intorno al 1450 Gutenberg stampa il primo libro della storia, una Bibbia) dà un forte impulso alla diffusione della conoscenza.
È il matematico tedesco Johannes Widmann a pubblicare per primo i simboli del + e del –, rispettivamente schematizzazione della p iniziale di plus e linearizzazione della m iniziale di minus.
Un secolo più tardi, nel 1557, il matematico gallese Robert Recorde introduce il simbolo dell’uguaglianza, concludendo un lungo e tortuoso cammino concettuale.
Seguiranno rapidamente gli altri simboli, fino a che, all’inizio del 1600 gli attrezzi di base, cifre e simboli, sono ragionevolmente stabili. Da lì si può partire a costruire l’edificio della matematica moderna.
Letture consigliate sulla rivoluzione dello zero e altre questioni:
C’era una volta un numero (George G. Joseph)
Storia dei simboli matematici. Il potere dei numeri da Babilonia e Leibniz (Joseph Mazur)
STORIA DELLA MATEMATICA (Carl B. Boyer)
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it