Parte il nuovo anno scolastico e per poco più di mezzo milione di studenti [1] arriva il momento dell’iniziazione al concetto di Teorema. I ragazzi sono quelli che cominciano la seconda media e a guidarli in questa esperienza sarà il teorema di Pitagora.
È un’iniziazione efficace o c’è il rischio di perdere una fondamentale occasione di formazione? Temo che sia, in molti casi, vera la seconda.
([1]: Dati dal sito Istat, qui il pdf)
Chi non conosce il teorema di Pitagora?
Credo che tutti abbiano un ricordo del teorema di Pitagora, e che molti riescano ad enunciarlo compiutamente:
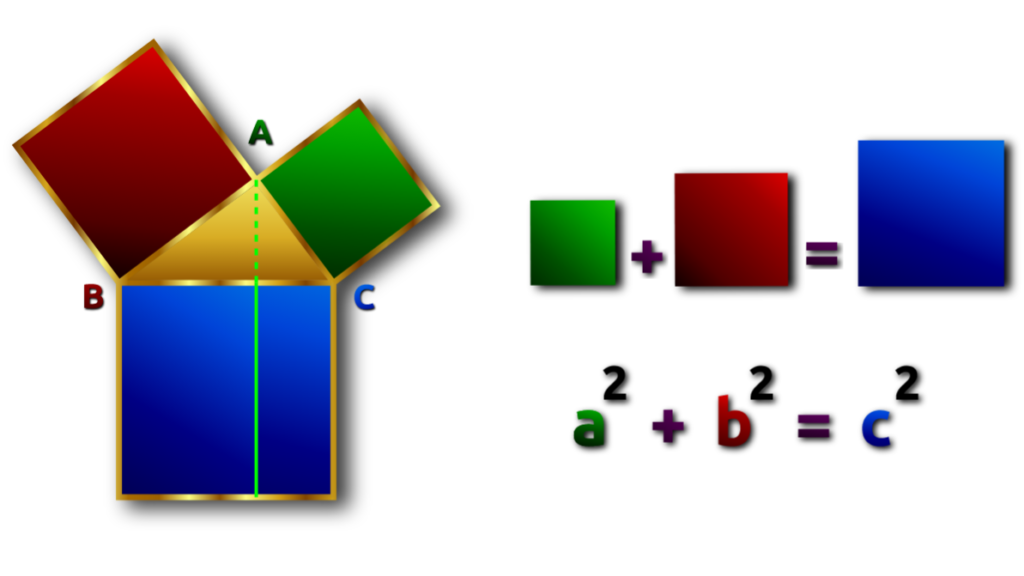
In ogni triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui due cateti.
Questo enunciato geometrico si esprime in termini matematici come: a2 + b2 = c2, dove a e b sono le misure dei cateti (cioè i lati dell’angolo retto) e c è la misura dell’ipotenusa (cioè il lato opposto all’angolo retto). In questa veste costituisce la parte semplice dell’ultimo teorema di Fermat.
Cos’è un teorema?
Capita di leggere sui giornali che il pubblico ministero Tizio avrebbe costruito un teorema contro Caio, con ciò intendendo che la tesi del pm è intenzionalmente priva di fondamento.
Se il giornalista e il signor Caio che si lamenta dell’ingiustizia avessero più proficuamente seguito il loro insegnante di matematica, non partorirebbero questo autentico autogoal, ma saprebbero invece che:
- ipotesi è il punto di partenza del ragionamento (se A, allora B);
- tesi è il punto a cui si vuole arrivare (se A, allora B);
- dimostrazione è la sequenza di passaggi logici inconfutabili che consente di arrivare da A a B;
- teorema è l’enunciato dimostrato vero (se A, allora B).
La padronanza di questi termini sarebbe già un buon risultato. Se poi i signori in questione avessero esagerato, allora saprebbero anche che:
- assioma è un punto di partenza assunto per vero, senza bisogno di dimostrazione (da qualche parte bisogna pur partire);
- corollario è una tesi dimostrata con semplici passaggi logici a partire da un altro teorema (una sorta di bonus);
- lemma è, al contrario, una tesi non rilevante di per sé, ma che spezza una lunga dimostrazione, consentendo di riprendere fiato.
(Per chi volesse approfondire)
Chi ha inventato i teoremi?
La storia del teorema di Pitagora è uno splendido esempio del percorso dell’umanità, dall’evidenza sperimentale alla capacità di astrazione e di deduzione rigorosa.
Nella storia della Geometria il punto di inizio del rigore sistematico è rappresentato dagli Elementi di Euclide, attivo intorno al 300 a.C. Discepolo di Platone, Euclide raccolse e sistematizzò la materia, partendo da cinque assiomi (o postulati).
Nell’800 si è aperto il filone delle geometrie non euclidee negando il quinto postulato:
data una retta e un punto esterno ad essa esiste un’unica retta parallela passante per detto punto.
Prima di Euclide si ragionava di geometria accontentandosi dell’evidenza delle conclusioni, senza andare troppo per il sottile. L’approccio era più che sufficiente per alzare mura solide, tirare su un’imponente piramide, ma senza l’ambizione dell’inconfutabilità assoluta. Anzi, senza nemmeno porsi il problema.
Chi è arrivato per primo al teorema di Pitagora?
La nozione di angolo retto è fondamentale nell’edificazione e nell’agrimensura (prima e forse unica occasione nella mia vita per usare questo termine). Si porta quindi dietro il problema di tracciare angoli retti sul terreno.
Gli Egizi affrontavano questo problema ad ogni piena del Nilo, dovendo ripristinare i confini di assegnazione dei campi.
Si servivano di un sistema pratico, basato sull’utilizzo di una semplice corda, che marcavano in 12 intervalli uguali mediante dei nodi. Perché 12? Semplice: 12 = 3 + 4 + 5, che sono le misure dei lati del più semplice triangolo rettangolo a lati interi. Era quindi sufficiente che tre uomini tendessero la corda tirandola dai nodi giusti, per poter tracciare sul terreno un angolo retto con ottima precisione.
Gli Egizi, manco a dirlo noti anche come tenditori di corde, avevano quindi grande dimestichezza con i triangoli rettangoli, come testimonia il Papiro di Rhind, risalente al 1650 a.C., ma la loro matematica aveva un approccio puramente operativo (vedi la pagina inglese di Wikipedia del Papiro di Rhind, problemi 51-52-53).
Non erano da meno i Babilonesi, come si deduce dalla Plimpton 322, tavoletta in argilla risalente al 1800 a.C. circa, su cui sono riportate le misure di diversi triangoli rettangoli a lati interi (tra cui quello di lati 3, 4 e 5 utilizzata dagli Egizi). Non vi è dubbio che i Babilonesi conoscessero i termini del teorema di Pitagora quindi, ma, anche per loro, si trattava di un risultato verificato operativamente e non raggiunto in modo rigorosamente deduttivo.
Ancora qualche secolo e si arriva a Pitagora, fondatore nel 530 a.C. della scuola pitagorica a Crotone. A lui si deve l’enunciazione del teorema, nei termini che conosciamo oggi.
Per la dimostrazione formale occorrerà però attendere ancora un po’, fino al nostro Euclide.
Dimostrazione del teorema di Pitagora
Non credo esistano teoremi con un numero di differenti dimostrazioni maggiore di quante se ne possano contare per il teorema di Pitagora. La questione è: ce ne sono alla portata di uno studente di seconda media?
Risposta: sì, almeno un paio. La prima che può venire in mente si basa sul primo teorema di Euclide:
“In ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l’ipotenusa e la proiezione di quel cateto sull’ipotenusa”.
Come si ragiona: divido il quadrato costruito sull’ipotenusa in due rettangoli, ciascuno dei quali è equivalente al quadrato costruito sul rispettivo cateto. Fatta!
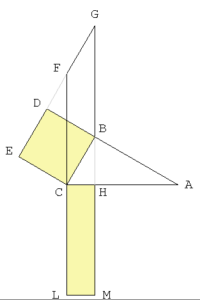
Rimane da dimostrare il primo teorema di Euclide, naturalmente. Ma questa è abbastanza semplice se si è già affrontato il calcolo dell’area dei parallelogrammi, perché allora ragiono così (vedi figura):
- CHML è equivalente a CFGB, visto con base CF;
- CFGB, visto con base CB è equivalente a CBDE.
Il dettaglio completo qui.
Ma c’è anche una dimostrazione più pratica
Per chi è arrugginito questa dimostrazione può sembrare complicata, ma in realtà non lo è: un allievo di seconda può essere guidato ad arrivarci. E il percorso, passando per l’area dei parallelogrammi e il primo teorema di Euclide, è decisamente formativo. Chi passa felicemente da qui dovrebbe avere ben chiaro il concetto di teorema.
Se, però, questa strada dovesse sembrare complessa, ce n’è un’altra che si presta anche a un approfondimento pratico, manuale.
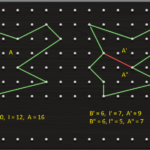
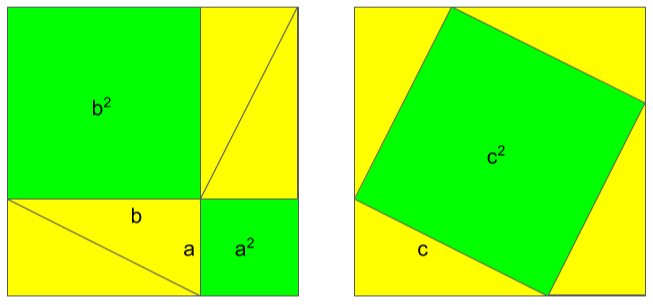
La dimostrazione era nota al matematico indiano Bhaskara (XII secolo). Come si procede (vedi figura):
- costruisco un quadrato con lato uguale alla somma dei cateti del triangolo rettangolo;
- all’interno dispongo in due modi diversi quattro copie del mio triangolo rettangolo, in modo da evidenziare:
- i due quadrati costruiti sui cateti;
- il quadrato costruito sull’ipotenusa.
È importante, però, che in questo ragionamento il volenteroso (?) studente venga guidato a comprendere che la proprietà che sta scoprendo non dipende dalla particolare forma del triangolo rettangolo, ma vale per tutti i triangoli rettangoli. Il teorema tratta la natura del triangolo (è rettangolo) e non particolari e specifici casi.
Quali dimostrazioni eviterei
Una tentazione in cui credo sia facile cascare è quella di semplificare, semplificare, semplificare, pur di ottenere attenzione e ascolto dai ragazzi.
Una semplice ricerca su Youtube ci offre diversi divertenti metodi di verifica sperimentale del teorema di Pitagora. Esempi: verifica basata sull’uso di perline colorate, piuttosto che sul travaso di liquidi.
Efficaci, senza dubbio. Però vedo difficile astrarre dalla procedura (che più manuale non si può) il concetto logico di dimostrazione. Approcci del genere potranno forse aiutare a memorizzare i termini del teorema (e nemmeno ne sarei troppo sicuro), ma non a radicare l’atteggiamento di rigore deduttivo.
Questo anno scolastico si apre con la novità, introdotta dalla Buona Scuola, dell’ eliminazione della bocciatura da elementari e medie (di fatto). Misura introdotta per ridurre la dispersione scolastica, e che allinea peraltro il nostro sistema scolastico a quelli più efficienti del nostro e coerentemente con le indicazioni degli esperti dell’OCSE in materia scolastica.
Giusto, bocciare non serve. Però occorre recuperare, e rapidamente, nei genitori prima che nei ragazzi, la reputazione dell’educazione scolastica: se il virgulto viene su rapa, tale rimarrà per la vita. Alla faccia della competitività che, c’è da scommetterci, diventerà sempre più feroce e divisiva.
Ma non vedo segnali positivi.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
